Diện tích hình tròn là gì? Công thức và bài tập vận dụng chi tiết

Bằng cách áp dụng công thức có sẵn, việc tính diện tích hình tròn sẽ đơn giản và dễ dàng hơn. Vì vậy, để biết công thức và cách giải bài tập tính diện tích hình tròn, các bạn hãy cùng Nguyễn Tất Thành tìm hiểu và giải đáp chi tiết trong bài viết sau nhé.

Ôn lại khái niệm về đường tròn

một vòng tròn là gì? Trong hình học phẳng, đường tròn là tập hợp tất cả các điểm cách một điểm cố định một khoảng bằng nhau. Điểm cố định đó được gọi là tâm của đường tròn và khoảng cách đó được gọi là bán kính của đường tròn.

Hình tròn có những đặc điểm sau:

• Các vòng tròn có tính chất đối xứng tròn.
• Đường kính của đường tròn là đoạn thẳng đi qua tâm và cắt đường tròn tại hai điểm đối diện.
• Độ dài đường kính gấp đôi bán kính hình tròn.

Công thức tính diện tích hình tròn

Trong tất cả các hình dạng trong toán học, hình tròn là một trong những hình có nhiều công thức tính toán nhất và là một chủ đề khá phức tạp. Trong đó, tính diện tích hình tròn là những kiến ​​thức mà học sinh cần nắm vững:

Ý tưởng

Diện tích của hình tròn được gọi là diện tích bên trong hình tròn, tỷ lệ với bình phương bán kính của nó.

Công thức tính diện tích hình tròn

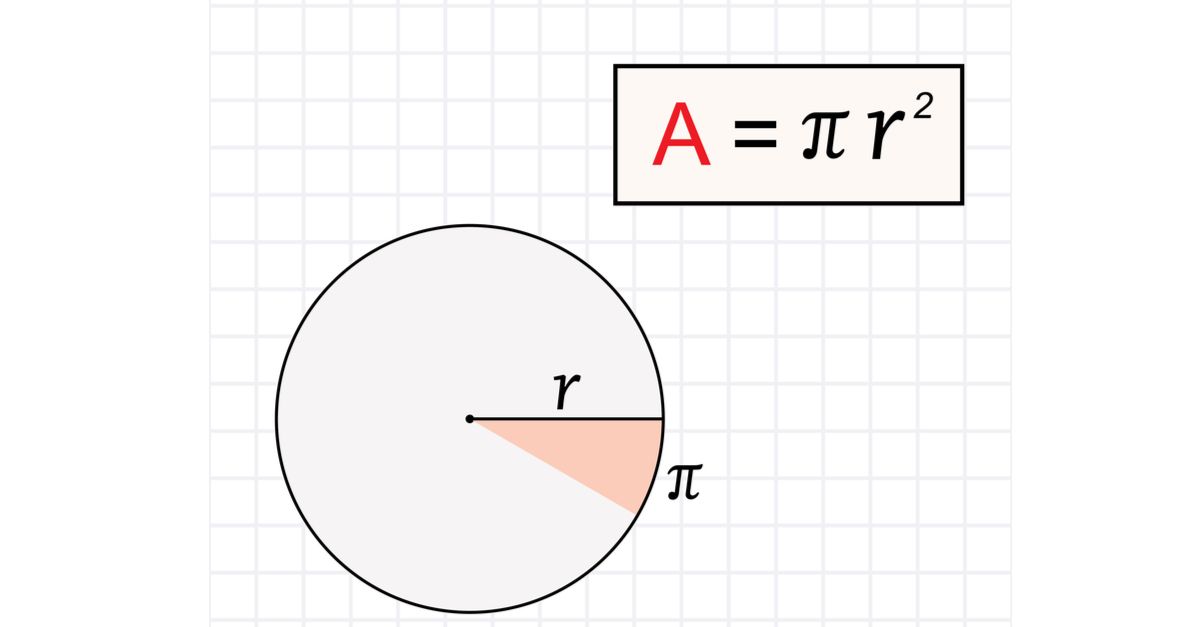
Để tính diện tích hình tròn người ta sẽ áp dụng công thức tích giữa số PI và bình phương bán kính hình tròn. Với, công thức tính diện tích hình tròn như sau:

S = πR2

Trong đó:

• S: là diện tích hình tròn

• π: là ​​số PI, với π = 3,14

• R: là bán kính hình tròn

Nhận xét: Để có thể tính diện tích hình tròn thì mọi người phải biết bán kính của hình đó. Một số đại lượng giúp bạn tìm bán kính hình tròn và tính S như sau:

Cách tính diện tích hình tròn

Tùy theo dạng bài tập yêu cầu tính S của đường tròn mà mỗi người sẽ có cách thực hiện khác nhau. Nhưng về cơ bản, quy trình sau sẽ được áp dụng.

Bước 1: Phân tích dữ liệu đã cho trong bài toán để tính S.

Nếu R được cho trong bài toán, chỉ cần áp dụng công thức S = πR2 hoặc S = S = π(d/2)2 để tính.

Nếu câu hỏi chưa đủ thông tin bạn sẽ chuyển sang bước 2.

Bước 2: Tìm dữ liệu còn thiếu => r

Nếu câu hỏi cung cấp thông tin về đường kính, để tính r, hãy áp dụng công thức r = d/2 (d là đường kính).

Nếu bài toán cho dữ liệu là chu vi của một hình tròn, để tìm r bạn sẽ áp dụng công thức r = C/(2.3,14)

Bước 3: Tìm câu trả lời

Từ bước 1 hoặc bước 2, sau khi tìm được r bạn chỉ cần áp dụng công thức tính S = πR2 để tìm ra đáp án đúng.

Trong trường hợp này, để tính diện tích nửa hình tròn, bạn chỉ cần áp dụng công thức S = πR2 và chia cho 2.

Cách tính diện tích nửa hình tròn

Diện tích hình bán nguyệt là một trong những cách tính hình tròn mà học sinh cần biết. Trong đó, diện tích hình bán nguyệt bằng một nửa diện tích hình tròn. Với, công thức tính sa hình tròn là S = πr^2, trong đó S là diện tích, π là số pi (khoảng 3,14) và r là bán kính hình tròn.

Vậy diện tích nửa hình tròn được tính theo công thức sau:

S = (πr^2)/2

Xem thêm : Gợi ý 10+ bài văn viết về ngày gia đình Việt Nam bằng tiếng Anh hay, ý nghĩa

Tóm lại, để tính diện tích nửa hình tròn, chúng ta cần thực hiện các bước sau:

Bước 1: Xác định bán kính hình tròn.

Bước 2: Áp dụng công thức S = (πr^2)/2 để tính diện tích.

Một số dạng bài tập phổ biến về tính diện tích hình tròn

Với kiến ​​thức về hình tròn sẽ có các bài tập liên quan đến tính diện tích như sau:

Dạng 1: Tính hình dạng đường tròn từ bán kính r hoặc đường kính d

Ở dạng bài tập này, dữ liệu sẽ được cho là r hoặc d và học sinh sẽ được yêu cầu tính diện tích hình tròn đó.

Về cách giải, bạn có thể dựa vào cách tính ở trên. Nếu cho r thì bạn chỉ cần áp dụng công thức S = πR2. Nếu cho d thì từ d => r và từ đó ta tính được s.

Ví dụ: Cho hình tròn C có đường kính d = 10 cm. Tính S của đường tròn C?

Giải: Ta có, bán kính bằng nửa đường kính theo công thức: R = d/2

=> R = 10/2 = 5cm

S đường tròn C: S = πR2 = 3,14,5,2 = 31,4 cm2

Dạng 2: Tính diện tích hình chiếc khăn

Dạng bài tập này sẽ cho một hình tròn có sẵn, bên trong hình tròn sẽ có một hình tròn nhỏ (hình chiếc khăn) và yêu cầu học sinh tính diện tích phần cần tìm đó của hình đó. Đồng thời dữ liệu sẽ cho biết bán kính của hình tròn lớn và bán kính hình tròn nhỏ để bạn có thể tìm ra đáp án chính xác.

Ví dụ: Cho hình vẽ, tính diện tích hình tròn màu xám. Biết, đường tròn nhỏ bên trong có r1 = 10cm, đường tròn lớn bên ngoài có r2 = 15cm.

Giải: Từ hình trên, diện tích vùng màu xám sẽ bằng hiệu của đường tròn S lớn với r2 và S đường tròn nhỏ với r1. Từ đó chúng ta có:

• S đường tròn nhỏ: S1 = πr12 = 3.14.102 = 314 cm2

• Diện tích hình tròn lớn: S2 = πr22 = 3.14.152 = 706,5 cm2

• Diện tích hình màu xám trong hình: S = S2 – S1 = 706,5 – 314 = 392,5 cm2

Dạng 3: Tính diện tích hình bất kỳ chứa 1 phần diện tích hình tròn

Đây là dạng bài tập nâng cao, khi đưa ra một hình vẽ tổng hợp nhiều hình khác nhau, trong đó có hình tròn và yêu cầu học sinh tính toàn bộ diện tích. Vì vậy, yêu cầu học sinh phải nắm vững các công thức tính các dạng toán khác nhau để dễ dàng giải được bài tập này.

Ví dụ: Tính diện tích toàn bộ hình dưới đây?

Giải: Diện tích toàn bộ hình trên sẽ bao gồm diện tích hình chữ nhật có kích thước 10 x 7cm, diện tích 2 nửa hình tròn bán kính r = 7.

• Diện tích hình chữ nhật: S1 = 10 x 7 x 2 = 140 cm2

• Diện tích hai nửa hình tròn có cùng bán kính: S2 = πR2 = 3,14,72 = 153,86 cm2

=> Diện tích toàn bộ ảnh: S = S2 + S1 = 140 + 153,86 = 293,86 cm2

Dạng 4: Bài toán nâng cao tính S từ d

Đây cũng là dạng bài tập toán đường tròn nâng cao, tùy theo dữ liệu cho trước để tìm bán kính hoặc đường kính rồi tính S.

Ví dụ: Tính hình S của một hình tròn, biết rằng nếu bạn tăng đường kính hình tròn lên 30% thì diện tích hình tròn sẽ tăng thêm 20 cm2.

Lời giải: Nếu bạn tăng đường kính hình tròn lên 30% thì bán kính cũng tăng 30%.

Phần trăm diện tích tăng lên là:

(130%)2 – (100%)2 = 69%

Vậy diện tích hình tròn ban đầu là: 20×100/69 = 29,956 cm2

Bài tập tính diện tích hình tròn để trẻ tự thực hành

Sau khi đã nắm vững kiến ​​thức lý thuyết về công thức và dạng bài tập, dưới đây Nguyễn Tất Thành sẽ tổng hợp một số dạng bài tập thường gặp trong đề thi để các bạn cùng luyện tập.

Bài tập trắc nghiệm

Bài tập tiểu luận

Mẹo giúp trẻ làm bài tập tính diện tích hình tròn hiệu quả

Đối với kiến ​​thức về hình tròn, đặc biệt là các bài tập về tính diện tích sẽ hơi phức tạp. Vì vậy, để giúp trẻ học và nắm bắt được những kiến ​​thức này, cha mẹ có thể áp dụng những mẹo sau:

Trang bị cho con bạn nền tảng toán học vững chắc với Nguyễn Tất Thành Math

Với những đứa trẻ không có niềm đam mê toán học và cha mẹ không có nhiều thời gian hỗ trợ, hãy thử lựa chọn Nguyễn Tất Thành Math để đồng hành cùng con bạn. Được biết, đây là ứng dụng học toán tiếng Anh hàng đầu tại Việt Nam, được nhiều phụ huynh không chỉ ở Việt Nam mà còn ở nhiều quốc gia khác lựa chọn để trang bị kiến ​​thức toán học và tăng thêm cảm hứng cho con em mình. .

Cụ thể, Nguyễn Tất Thành Math cung cấp nội dung toán học bám sát chương trình giáo dục mới nhất, nhằm thúc đẩy trẻ phát triển hơn khả năng toán học, tích cực học tập, tư duy và nắm bắt gốc rễ của các bài toán.

Đặc biệt, toàn bộ chương trình giảng dạy tại Nguyễn Tất Thành Math còn dựa trên American Common Core State Standards, với hơn 60 chủ đề toán học, dựa trên 7 chủ đề chính bao gồm:

• Đếm & Thu thập số

• Giải tích & Tư duy đại số

• Số thập phân & phép tính

• Đo lường

• Hình học

• Không gian & Thời gian

• Dữ liệu & Đồ thị

Đặc biệt, mọi thứ sẽ được chia thành 4 cấp độ học từ dễ đến nâng cao phù hợp với nhiều lứa tuổi và trình độ của trẻ. Vì vậy cha mẹ có thể dễ dàng lựa chọn trình độ học tập phù hợp nhất với con mình.

Đặc biệt, hệ thống bài học trong Nguyễn Tất Thành Math được thiết kế logic, chặt chẽ với các hoạt động học tập và ôn tập kiến ​​thức. Qua đó giúp trẻ dễ dàng lĩnh hội và tiếp thu chúng một cách hiệu quả hơn.

Thay vì những bài học khô khan từ sách vở, khi học với Nguyễn Tất Thành Math, trẻ sẽ được trải nghiệm, khám phá nhiều hoạt động thông qua các trò chơi tương tác, xem video bài giảng, giải câu đố, làm bài tập,… với những hình ảnh minh họa ngộ nghĩnh, âm thanh sinh động nhằm cung cấp kiến ​​thức một cách trực quan và giúp ích cho trẻ. tiếp thu kiến ​​thức một cách hứng thú và tự nhiên nhất.

Tải Nguyễn Tất Thành Math cho điện thoại Android

Tải Nguyễn Tất Thành Math cho điện thoại iOS

Nắm chắc kiến ​​thức liên quan đến tính diện tích hình tròn

Khi học bất kỳ kiến ​​thức nào, học sinh cần nắm chắc phần đó. Khi học diện tích hình tròn, cha mẹ cần kiểm tra xem con mình đã nắm vững các kiến ​​thức liên quan như bán kính, đường kính, chu vi hình tròn, công thức tính,…

Bởi vì chỉ khi hiểu rõ tất cả những sự thật này, trẻ mới có thể chinh phục được phép tính diện tích hình tròn một cách chính xác.

Luyện tập cùng con và luyện tập thường xuyên

Để tránh tình trạng trẻ “học trước quên sau”, cha mẹ nên luyện tập cùng con thường xuyên. Việc thực hành ở đây có thể đến từ việc cùng con làm bài tập trong sách giáo khoa, học nhiều kiến ​​thức trên mạng để nâng cao kỹ năng, tổ chức các cuộc thi nhỏ, học qua trò chơi,…

Khi luyện tập và thực hành thường xuyên, trẻ sẽ ghi nhớ tốt hơn, cũng như có hứng thú với quá trình học tập.

Xem thêm:

1. Nguyễn Tất Thành Math – Ứng dụng học toán bằng tiếng Anh số 1 dành cho trẻ mẫu giáo & tiểu học
2. Cách tính bán kính hình tròn đơn giản và bài tập tự luyện hiệu quả
3. Cách tính đường kính hình tròn đơn giản chỉ với 3 công thức

Ghi nhớ công thức vòng tròn qua bài thơ

Dưới đây là bài “thơ” về công thức hình tròn để trẻ có thể học và ghi nhớ dễ dàng hơn:

Diện tích hình tròn đơn giản

Bình phương bán kính và nhân nó ngay lập tức

Ba phẩy mười bốn phía sau

Chu vi cũng dễ dàng tính toán nhanh chóng

Đường kính chúng tôi lấy ra lõi

Ba phẩy mười bốn, thế là xong.

– Sưu tầm –

Kết luận

Trên đây là thông tin về diện tích hình tròn. Tuy đây chỉ là kiến ​​thức cơ bản nhưng nó là công cụ để bạn giải các bài tập nâng cao nên hãy nắm bắt thật kỹ và đừng bỏ qua những mẹo mà Nguyễn Tất Thành gợi ý để hỗ trợ quá trình làm bài. Học tập hiệu quả hơn.

Nguồn: https://truongnguyentatthanh.edu.vn
Danh mục: Giáo dục