Các dạng bài tập đạo hàm lớp 11 hướng dẫn giải chi tiết dễ hiểu nhất

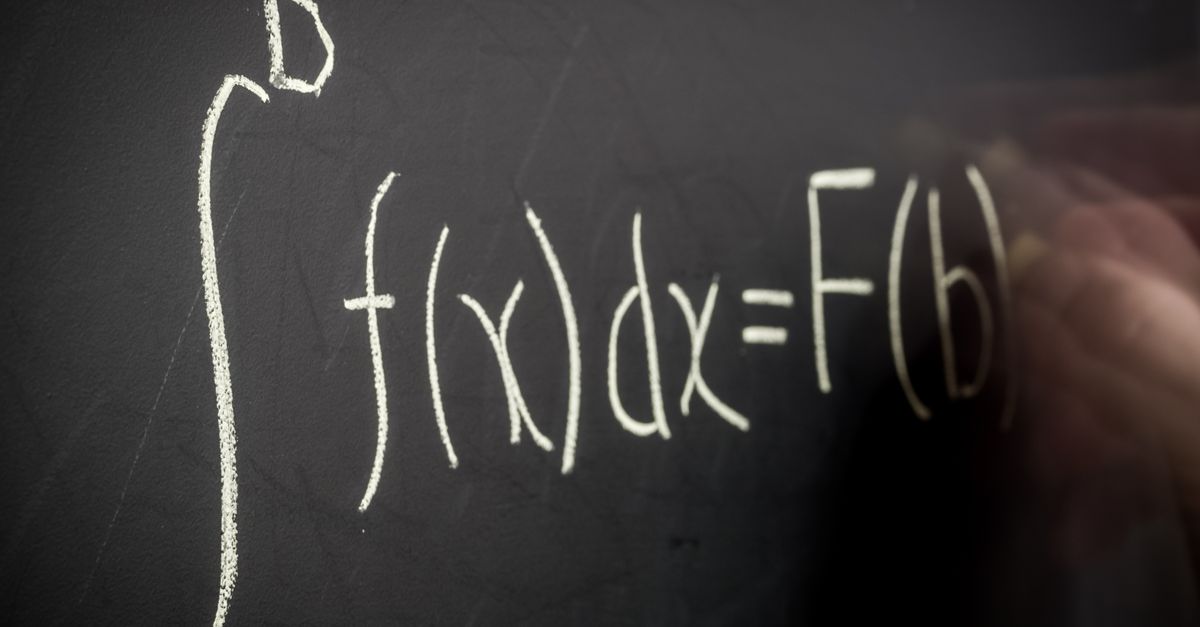
Đạo giáo là một hình thức kiến ​​thức toán học lớp 11 thường được bao gồm trong các bài kiểm tra quan trọng từ học kỳ, kỳ thi quốc gia, kỳ thi trung học, kỳ thi đại học. Do đó, việc xem xét và giải các bài tập chức năng thường xuyên là một giải pháp giúp học sinh đạt được kết quả cao cho chính họ.

Do đó, con khỉ nội dung sau đây sẽ chia sẻ các loại bài tập về tôn giáo chức năng 11 lớp với giải pháp cho mọi người tham khảo và áp dụng.

Bạn đang xem: Các dạng bài tập đạo hàm lớp 11 hướng dẫn giải chi tiết dễ hiểu nhất

Một số sai lầm khi giải các bài tập phái sinh mà học sinh nên tránh

Trong quá trình học tập, giải quyết các bài tập về phái sinh lớp 11, họ thường mắc một số sai lầm vì chúng không nắm bắt được kiến ​​thức cơ bản như:

• Sự đơn điệu của hàm là trên một phạm vi.
• Không hiểu định nghĩa chính xác của một điểm quan trọng của hàm khi tính toán đạo hàm.
• Điều kiện chức năng đơn điệu trên khoảng hoặc dẫn xuất của các thái cực tại một điểm x0
• Giá trị tối thiểu, tối đa của hàm trên Dominatom khi tính toán đạo hàm.
• Sự khác biệt giữa tiếp tuyến tại một điểm của biểu đồ dựa trên tiếp tuyến từ 1 điểm đến một biểu đồ nhất định.
• Sự đơn điệu của dẫn xuất chức năng.
• Điểm quan trọng của hàm, vì vậy khi xem xét trạng thái của hàm, ‘thường bị nhầm lẫn.
• Áp dụng sai các thuộc tính khi tính toán đạo hàm của hàm nghịch đảo và thống nhất.
• Áp dụng sai công thức để tính toán đạo hàm, hoặc đạo hàm tại một điểm.
• Chưa nắm bắt được kiến ​​thức cơ bản đã học được đạo hàm tiên tiến.

Các loại bài tập chức năng phổ biến nhất 11

Một trong những yếu tố quan trọng khi giải pháp chức năng 11 là nắm bắt các hình thức toán học phổ biến, để áp dụng giải pháp chính xác chính xác hơn.

Cụ thể, các bài tập phái sinh thường sẽ có các hình thức cơ bản sau:

Mẫu 1: đạo hàm bằng với định nghĩa

Đây được coi là một trong những hình thức toán học chính thức cơ bản nhất. Họ chỉ cần dựa vào định nghĩa để có thể áp dụng và tính toán chính xác. Cụ thể:

Mẫu 2: Chứng minh sự công bằng của đạo hàm

Một trong những hình thức phái sinh này sẽ tập trung vào việc chứng minh một hệ thống dựa trên một điều kiện nhất định. Nó đòi hỏi trẻ em phải chứng minh và tính toán chúng để kết quả cuối cùng là.

Mẫu 3: Viết phương trình tiếp tuyến khi biết liên hệ

Đây là một trong những loại bài tập phái sinh cấp 11 phổ biến nhất. Cụ thể, sẽ có một phương trình tiếp tuyến của hàm trên biểu đồ của đường cong (c): y = f (x) tại tiếp xúc m (x0; y0) có dạng: y = y = y ‘(x0) ( X-X00.

Ví dụ: Cho hàm y = x3 + 3mx2 + (m + 1) x + 1 (1), m là một tham số thực. Tìm các giá trị của M để tiếp tuyến với đồ thị của hàm (1) tại điểm với tọa độ x = -1 đi qua điểm A (1; 2).

Xác định bộ d = r

y ‘= f’ (x) = 3×2 + 6mx + m + 1

Cho x0 = -1 => y0 = 2m -1, f ‘(-1) = -5m + 4

Phương trình tiếp tuyến tại điểm m (-1; 2m -1): y = (-5m + 4) (x + 1) + 2m -1 (d)

Chúng ta có A (1; 2) (d) (-5m + 4) .2 + 2m -1 = 2 => m = 5/8

Mẫu 4: Viết phương trình tiếp theo khi biết hệ số góc

Xem thêm : Cách phát âm b: Chữ b trong tiếng Anh đọc thế nào? (Audio + VD)

Viết phương trình tiếp tuyến Δ của (c): y = f (x), biết Δ có góc k

Đặt m (x0; y0) là liên hệ. Tính toán y ‘=> y’ (x0)

Vì phương trình tiếp tuyến có hệ số góc k => y ‘= (x0) = k (i)

Giải quyết (i) Tìm x0 => y0 = f (x0) => Δ: y = k (x – x0)+ y0

Lưu ý: Hệ số góc k = y ‘(x0) của tiếp tuyến thường là gián tiếp như sau:

Ví dụ: cho hàm y = x3+3×2-9x+5 (c). Trong tất cả các tiếp tuyến của đồ thị (C), tìm tiếp tuyến với hệ số góc nhỏ nhất.

Chúng ta có y ‘= f’ (x) = 3×2 + 6x – 9

Đặt x0 là tọa độ tiếp xúc của tiếp tuyến, vì vậy f ‘(x0) = 3 x02 + 6 x0 – 9

Chúng ta có 3 x02 + 6×0 Từ 9 = 3 (x02 + 2×0 +1) – 12 = 3 (x0 + 1) 2 trận 12> – 12

Vì vậy, Min F (x0) = -12 tại x0 = -1 => y0 = 16

Đã suy ra phương trình tiếp tuyến để tìm: y = -12 (x+1) +16 y = -12x+4

Mẫu 5: Phương trình và phương trình với đạo hàm

Trong hình thức toán học này sẽ kết hợp nhiều công thức để giải phương trình hoặc sự bất bình đẳng được đưa ra và tính toán số cuối cùng.

Mẫu 6: Tính toán đạo hàm theo công thức

Ở đây chúng cần thuộc về các công thức chức năng cơ bản để có thể giải quyết các bài tập một cách chính xác. Trong trường hợp, nếu bạn thấy các chức năng phức tạp, bạn có thể rút ngắn trước chức năng trước khi tiến hành dẫn xuất, đặc biệt là nội dung lượng giác.

Mẫu 7: Phương trình tiếp tuyến của biểu đồ hàm tại một điểm nhất định của biểu đồ hoặc một hệ số góc đã cho

Khi thực hiện bài tập chức năng này, sinh viên cần phải thành thạo hai hình thức tiếp tuyến cơ bản sau:

Mẫu 8: phái sinh cấp cao

Ở dạng các bài tập phái sinh cấp 11 cấp cao thường ủng hộ cấp 2 trở lên, tại thời điểm này, chúng có thể áp dụng công thức y (n) = (y (n-1)) ‘.

Trong trường hợp tính toán mức N và học sinh, họ sẽ phải tính toán đạo hàm từ cấp 1, 2, 3, …. và sau đó tìm công thức tính toán chức năng của cấp độ n. Thường có thể áp dụng phương pháp quy nạp toán học để chứng minh rằng công thức là đúng.

Một số bài tập phái sinh có giải pháp cho học sinh thực hành

Xem thêm : Hướng dẫn cách giúp bé học đánh vần chữ ghép dễ hiểu, dễ học

Để có thể giải quyết các bài tập phái sinh chính xác 11 chính xác, nó đòi hỏi trẻ phải thực hành nhiều bài tập về nhà hơn. Kết hợp với việc làm chủ các công thức, quy tắc và định dạng toán học, chương chức năng chắc chắn sẽ không còn gây khó khăn cho bạn nữa.

Vì vậy, đây là một số bài tập khỉ nói chung cho trẻ em tự giới thiệu và thực hành:

Làm thế nào để giải tập bài tập phái sinh lớp 11?

Để có thể vượt qua những sai lầm trên, nó đòi hỏi trẻ em phải thực hành rất nhiều. Ngoài ra, mọi người có thể áp dụng một số phương pháp hiệu quả ngay tại đây:

Hiểu công thức và định nghĩa của đạo hàm

Trong đại số lớp 11, phái sinh được coi là một chủ đề quan trọng mà họ cần chú ý. Bởi vì đây là một hình thức toán học xuất hiện trong tất cả các bài kiểm tra từ học kỳ, trung học, trường đại học và ngay cả khi học đại học vẫn gặp lại họ.

Do đó, để tìm hiểu phái sinh trước tiên, mọi người phải hiểu suy nghĩ, công thức và quy tắc trong tính toán phái sinh. Tất nhiên, họ không nên học vẹt mà không hiểu.

Thay vào đó, họ nên đọc công thức, mổ xẻ từng định nghĩa, định lý và biết cách áp dụng từng công thức vào từng loại bài tập. Để giúp học hỏi nhanh, hiểu sâu sắc và các quy tắc và công thức, trẻ em nên là hệ thống cũng như về chúng theo các nguyên tắc như trật tự, hình thức toán học …

Thực hành giải các bài tập phái sinh lớp 11 từ cơ bản đến nâng cao

Nếu chỉ hiểu công thức, quy tắc là không đủ. Nếu họ không dành thời gian áp dụng chúng vào các bài tập phái sinh cụ thể, chúng cũng sẽ là “học vẹt”. Đó là thực hành giải quyết các bài tập thường xuyên là công cụ giúp trẻ có được kiến ​​thức chương chức năng này tốt hơn.

Hiện tại, có nhiều loại khác nhau từ các bài tập phái sinh cơ bản đến nâng cao. Các dẫn xuất từ ​​định nghĩa, công thức, đồ thị tiếp tuyến, các dẫn xuất cao … Mỗi hình thức có vấn đề từ đơn giản đến phức tạp.

Do đó, họ cần hiểu các loại bài tập trong sách giáo khoa, tài liệu toán học, bài tập nhìn thấy cô ấy …. từ đó mọi người sẽ thực hành thường xuyên với họ để hiểu và thực hành nhiều hơn.

Đọc hiểu điều kiện khi giải các bài tập toán học

Trong toán toán, sẽ luôn có điều kiện để giải quyết số lượng bài toán. Do đó, họ cần đọc và hiểu các điều kiện khi giải các bài tập một cách chính xác.

Sẽ không có điều kiện cho một vấn đề phái sinh bình thường. Nhưng yêu cầu thường nằm trong phần câu hỏi phụ như giải quyết giải pháp của phương trình, … từ đó tạo ra một tiền đề để giải các bài tập đúng dựa trên các điều kiện đó.

Vẽ kinh nghiệm và giải quyết các bài tập phái sinh của riêng họ

Với việc học toán nói chung, kiến ​​thức phái sinh nói riêng, trẻ em có thể học hỏi từ sách giáo khoa, giáo viên, bạn bè, gia sư … nhưng đó là phương pháp học tập tốt nhất là phương pháp học tập tốt nhất. .

Đặc biệt, bạn không nên quá phụ thuộc vào giáo viên hoặc sách. Trong quá trình thực hiện bài tập hàm thường xuyên, bạn chắc chắn sẽ tự phát hiện mình ở nơi bạn thường sai, từ đó sẽ dễ dàng rút ra trải nghiệm và bài học của riêng bạn.

Bên cạnh đó, trong toán học toán học, cũng có các công thức được tính toán nhanh, các mẹo để xác định các bài tập … do đó, họ nên biết các thủ thuật này để giải quyết toán học một cách hiệu quả, nhanh chóng và chính xác.

Luôn kiên trì và thực hành nhiều bài tập

Thực tế là họ hiểu bản chất của phái sinh, chỉ cần kết hợp với sự kiên trì, thực hiện nhiều bài tập chắc chắn không khó. Vì vậy, hãy dành thời gian để thực hiện tất cả các bài tập trong sách giáo khoa, các bài tập cũng đã nắm bắt được 80 – 90% các kỹ năng để giải quyết bài tập phái sinh.

Ngoài ra, học hỏi từ giáo viên, bạn bè và bản thân họ tóm tắt kinh nghiệm cũng sẽ giúp họ phát hiện những thiếu sót để vượt qua và thúc đẩy tốt hơn.

Một số ghi chú khi giải bài tập về lớp 11

Để có thể giải quyết bài tập chức năng tăng chính xác hơn, họ cần chú ý đến một số vấn đề sau:

• Đào tạo rất nhiều bài tập để tóm tắt kinh nghiệm của riêng bạn.
• Có một thái độ chăm chỉ, dai dẳng và không thoải mái.
• Ngoài kiến ​​thức về sách giáo khoa, trên trường có thể học được phái sinh trên internet để học và kinh nghiệm.
• Học giới hạn của chức năng sẽ giúp bạn nhớ công thức phái sinh nhanh hơn và tốt hơn.
• Không ngại trao đổi với giáo viên, phụ huynh, bạn bè nếu có khó khăn trong đức hạnh

Xem thêm: Hàm 1/x là gì? Các loại bài tập và giải pháp phái sinh của 1 phần chi tiết nhất x

Kết luận

Với việc chia sẻ ở trên, nó phải giúp mọi người nắm bắt loại bài tập hàm 11 lớp chung. Hy vọng, dựa trên kiến ​​thức đó, nó sẽ giúp họ ít lo lắng và đủ tự tin để chinh phục chương chức năng dễ dàng hơn. Mong muốn thành công.

Nguồn: https://truongnguyentatthanh.edu.vn
Danh mục: Giáo dục